Area of Trapezoids made easy.
/Above: Two different formulas to find Area of Trapezoids
The Trapezoid
In the world of quadrilaterals, the formula to find area of Trapezoids is one of the most feared by middle school students. Perhaps it’s the use of parentheses. If you throw these bad boys into a problem it’s sure to create a certain level of anarchy. Possibly it’s the use of the numbers 1 and 2 written below and to the right of the two bases (b) in the parentheses.
Regardless of of the reason, the formula for Area of Trapezoids has caused many kids to surrender without so much as a fight.
The kicker is that the formula is not difficult to solve. In this blog we will look at a couple of the key terms, dissect the formula, give three examples of finding area and show you a few ways to model finding the area.
Key Terms
There are two key terms in the world of the Trapezoid: Bases and Height.
The Bases are two sides that are parallel. Trapezoids have only one set of parallel sides. The Height can also be thought of as the distance between the bases. In most examples, the two bases are on the top and the bottom, but if you rotate the trapezoid 90 degrees the bases are now on the right and left sides.
Area of Trapezoid Formula
There are two common formulas that you will see used when finding the area of a trapezoid:
Area = 1/2 (Base 1 + Base 2) x height or
Area = (Base 1 + Base 2) divided by 2 x height
It’s important to understand that dividing by 2 and multiplying by 1/2 are the same thing. For example, 10 divided by 2 equals 5 and 10 times 1/2 also equals 5.
What is helpful to understand is that 1/2 (Base 1 + Base 2) and (Base 1 + Base 2) divided by 2 are both just ways of finding the average of the two bases. You can think of this as the Mean or the Median it doesn’t matter. So really Area of a Trapezoid is just the Average of the Bases x Height (or the distance between the bases)
3 Examples of Finding area of Trapezoids
Example #1
In this example we have a trapezoid with a bases of 13 and 7 and a height of 3. First we add up our bases to get 20 (13 + 7). Next we multiply 20 by 1/2 to get 10. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 10 (which is the average of the two bases) and multiply it by the height (3) to find the area of this trapezoid which is 30 square units.
Example #2
In this example we have a trapezoid with a bases of 10 and 6 and a height of 6. First we add up our bases to get 16 (10 + 6). Next we multiply 16 by 1/2 to get 8. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 8 (which is the average of the two bases) and multiply it by the height (6) to find the area of this trapezoid which is 48 square units.
Example #3
In this example we have a trapezoid with a bases of 10 and 6 and a height of 3. First we add up our bases to get 16 (10 + 6). Next we multiply 16 by 1/2 to get 8. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 8 (which is the average of the two bases) and multiply it by the height (3) to find the area of this trapezoid which is 24 square units.
3 Ways to model Finding the area of Trapezoids
Example #1
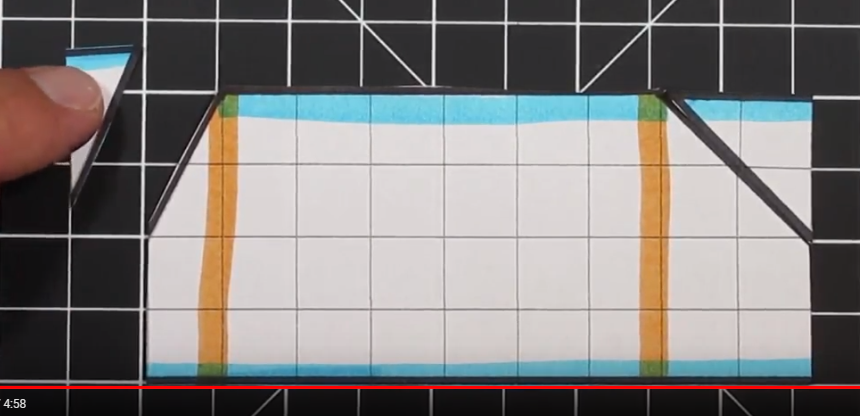
This is an example of a Trapezoid when the “triangles” are the same on both sides.
One of the goals of modeling area of a trapezoid is to show how we can convert a trapezoid into a rectangle. In the above example, we have two equal “triangles” on each side. This trapezoid has bases of 12 and 4 with a height of 4.
First, we can cut off one of the two triangles. We are then going to move it to the other side.
Once we move the triangle from one side to the other (in this example right to left) we can arrange the triangle to fit perfectly and form a rectangle. In this example an 8 x 4 rectangle is created which has an area of 32 units squared.
Example #2
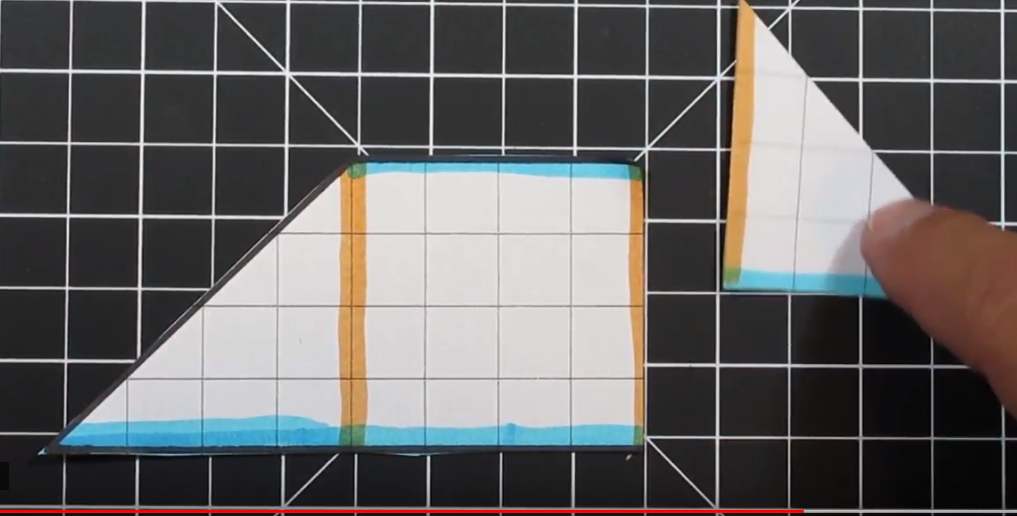
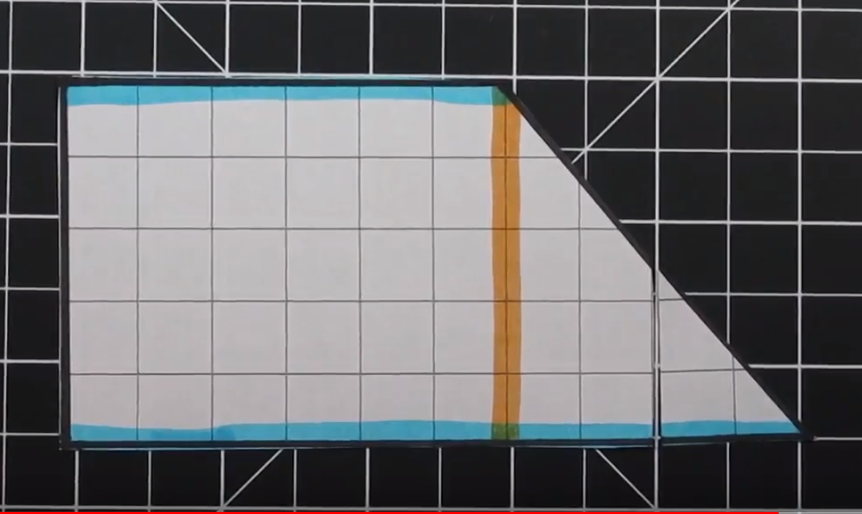
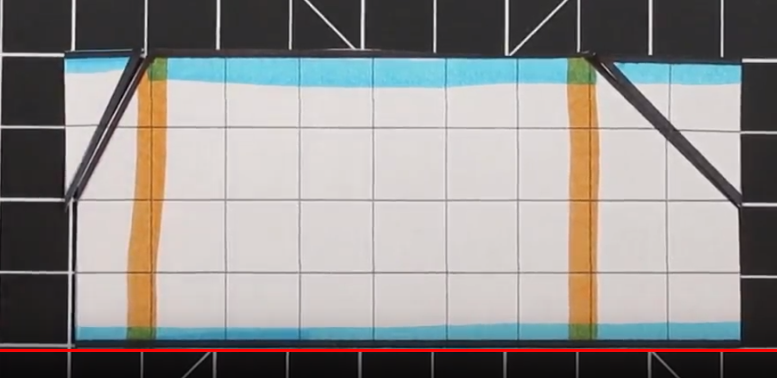
This is an example of a trapezoid with two right angles. As a result there is only one “triangle.”
This Trapezoid has two right angles on the left side. There is a triangle on the right side. The Trapezoid has bases of 6 (on top) and 10 (bottom) along with a height of 5.
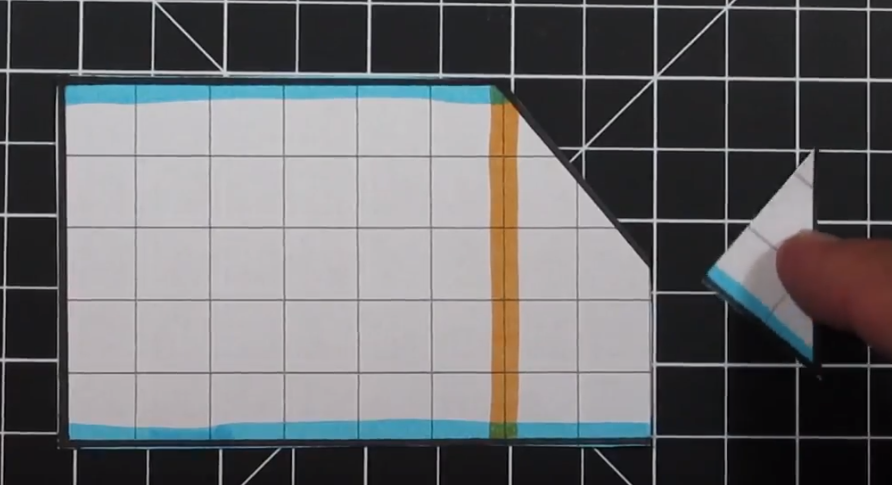
To transform this trapezoid into a rectangle we are going to cut the triangle in half (half of the base of the triangle). Next we are going to take the piece we cut off and move to the upper right to create a rectangle.
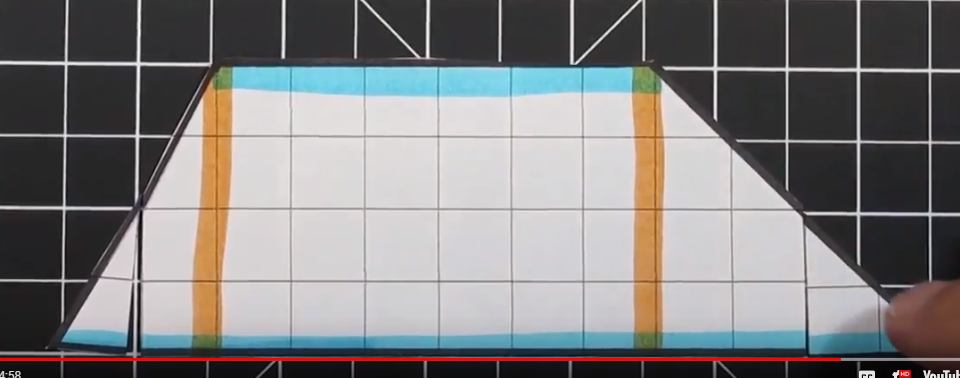
Finally, once we rearrange the trapezoid we can create a rectangle with a base of 8 and a height of 5. This equals an area of 40 cm squared.
Example #3
This an example of a trapezoid with triangles on each side, but both have a different base.
This trapezoid is similar to the trapezoid in Example #1. The big difference is the two triangles have a different base. So just like in Example 2, we are going to need to cut both triangles in half.
In this example, we are cutting the triangle on the right side in half and rearranging it .
Next, we do the same thing to the triangle on the left side.
Once we rearrange the trapezoid, a rectangle with a base of 9 and height of 4 has been created. The area is 36 square units which is easy to see when we rearrange the trapezoid.
Watch the Video !
Check out: Finding the Area of Unique Shapes.
A collection of 44 different Shapes using triangles, quadrilaterals (including trapezoids) and circles.