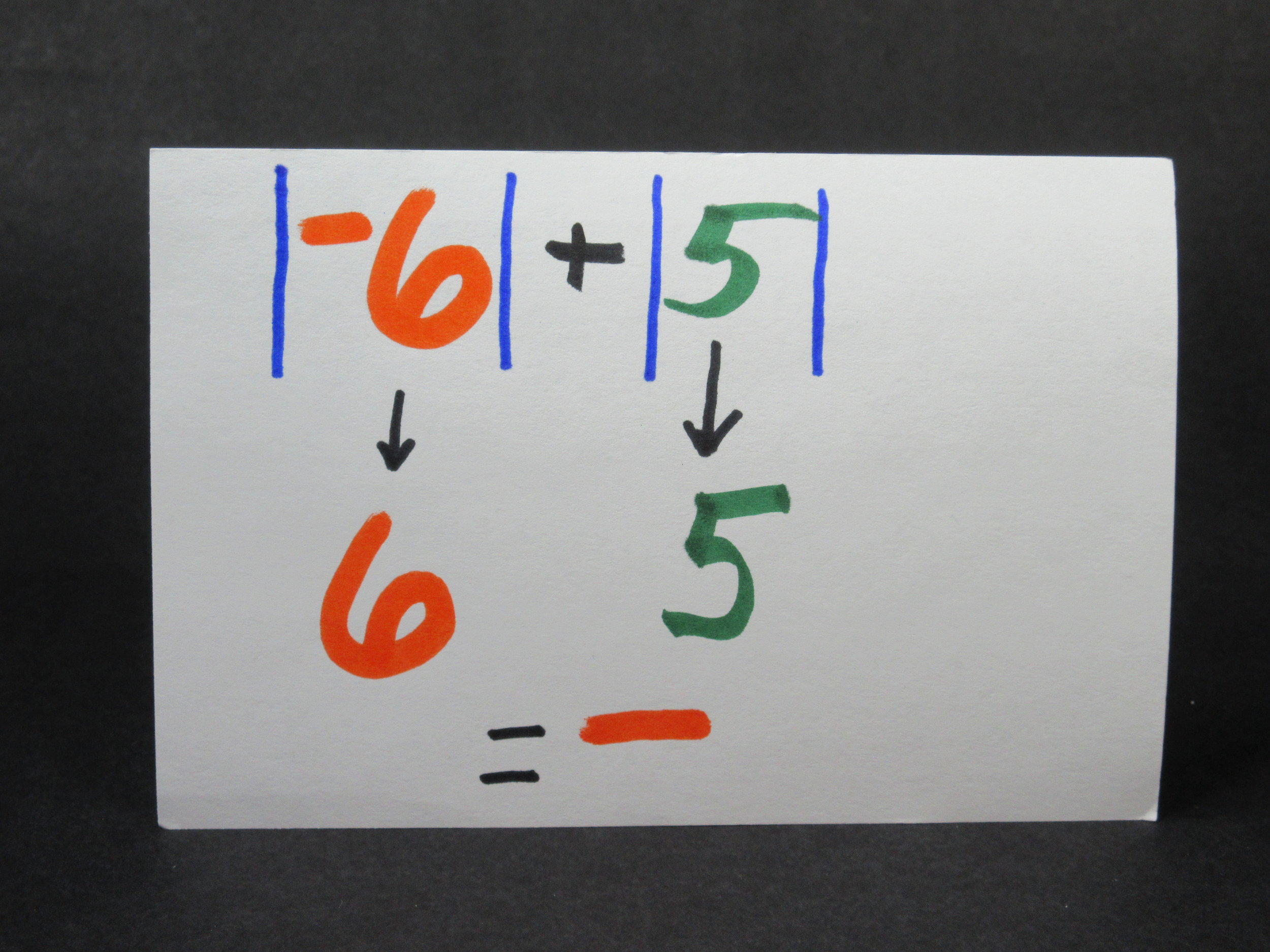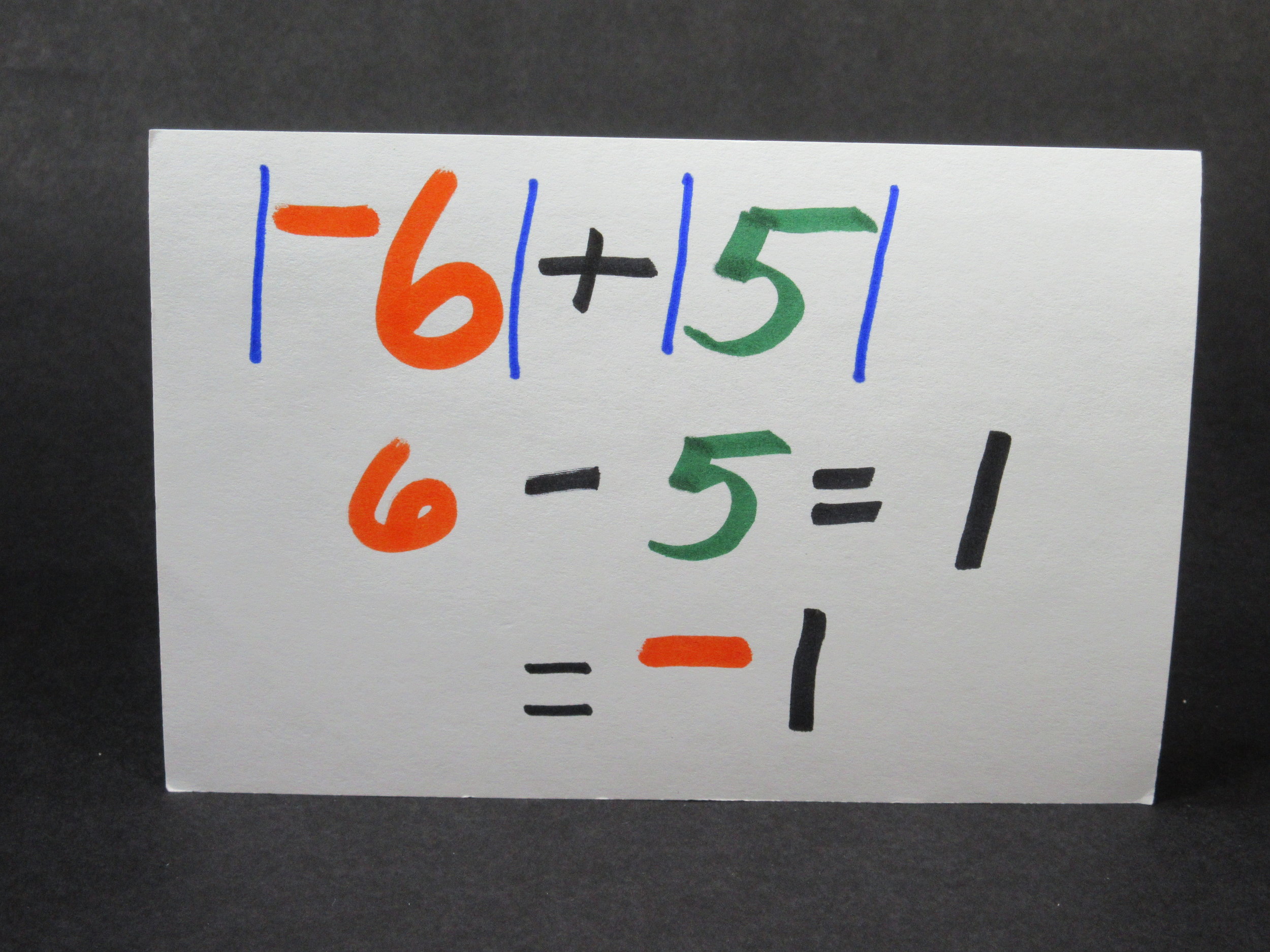Watch the video of Green vs. Tan Soldiers in this struggle to help you understand how to add and subtract integers.

In the land of math, one of the greatest challenges is understanding how to add and subtract integers (positive and negative numbers). Anytime you are engaged in an epic struggle it’s always a good thing to bring in reinforcements. Battling Integers is no exception.

To help us tip the odds in our favor we have brought in a group of elite mathematical warriors. The heros we are speaking of are the legendary toy army soldiers. These bitter rivals (tan and green soldiers) have united with the common goal of leading us to victory in the struggle with adding and subtracting integers.

The Rivals: Green (positive) vs. Tan (Negative)

Anytime you add two opposite numbers you always get zero.

In this conflict the Green army soldiers will represent positives and the Tan army soldiers will represent negatives. A critical concept to understand is that if you add a positive one and a negative one together you get zero. Any time you add opposites you will always get zero.

For example, a +7 + -7 = 0 and +29 + -29 = 0.

Operation Addition

Positive + Positive = Positive

This first situation is by far the easiest. This is what we were taught back in elementary school. Back in elementary school your teacher probably didn’t refer to the numbers you were adding as positives, but they were. So, 2 + 1 = 3 is really a +2 + +1 = +3.

Two Pieces of trivia to help you:
1) Many times numbers will be put into parenthesis. So, +2 + +1 = +3 might be written as (+2) + (+1) = (+3).
2) If a number doesn’t have a sign (example: 8 + 2 = 10) it is understood that the number is a positive. So in this example, the 8, 2, and 10 are all positives because there is no sign.

If we are adding two positive numbers I like to think of this as green soldiers (the positives) are getting reinforcements. For example, if we start with 5 green army soldiers (+5) and three more green soldiers (+3) join them we now have a total of 8 green (+8) soldiers. When you add a Positive + Positive you will always get a Positive answer.

We start with 5 green soldiers which represents a +5

3 more green soldiers (+3) are added to the battle.

Negative + Negative = Negative

This is very similar to the previous example.

If we are adding two negative numbers I like to think of this as the tan soldiers (the negatives) are getting reinforcements. For example, if we start with 4 tan army soldiers (-4) and three more tan soldiers (-3) join them we now have a total of 7 tan (-7) soldiers. When you add a Negative + a Negative you will always get a Negative answer.

We start out with 4 tan soldiers which represents a negative 4

3 more tan soldiers (-3)are added to the mix

Adding Positive and Negative

When you are adding a positive and a negative things get a bit more challenging. When you are adding different signs you can get either a positive or a negative answer. This is where the Army soldiers really help us to model this.

Two questions to ask yourself when adding a positive (green soldiers) and a negative (tan soldiers).

Which side has the advantage? In other words, which side has the most soldiers? The side that has the most soldiers will be the sign of the answer. For example, if you have more tan soldiers you will have a negative answer.
How many more soldiers does the one side have over the other? This difference is the number that will go with the sign.

Positive + Negative = Positive

In our first battle we have 3 green soldiers (+3) and 2 tan soldiers (-2). In this fight the green soldiers (the positives) have the advantage. So this means the answer to this problem will be a positive answer. Next, we look at the advantage the green soldiers have in this battle which is a 1 soldier advantage. As a result, the answer to (+3) + (-2) = (+1).

The 2 tan soldiers and 2 of the green soldiers when combined equal zero. The only thing that is left standing is the lone green soldier.

2 Tan soldiers (-2) are then added to the fight

The result of adding to Tan soldiers (-2) to 3 green soldiers (+3) is a 1 soldier advantage for the green (+1).

Other examples:

(+8) + (-2) = (+6)

(+31) + (-15) = (+16)

Positive + Negative = Negative

In out next clash, we have 2 green soldiers (+2) and 6 tan soldiers (-6). In this battle the tan soldiers have the advantage, so we know the answer is going to be a negative because we have more tan soldiers. When we compare the two sides, the tan soldiers (negatives) have the advantage by 4 soldiers. So we know the answer is going to be: -4. So, (+2) + (-6) = (-4).

The 2 green soldiers and 2 of the tan soldiers cancel each other out (equal zero). All we are left with is the 4 tan soldiers.

We add 6 tan soldiers (-6) to the battle

the result of adding the 6 tan soldiers (-6) to the 2 green soldiers (+2) is an advantage for 4 more tan soldiers (-4)

Other examples:

(+4) + (-9) = (-5)

(-34) + (+25) = (-9)

RULES FOR ADDITION

When adding two numbers with the same sign
1. Keep the sign
2. Add the numbers
When adding two numbers with different signs
1. Use the sign that you have the most of
2. Find the difference in the amount of Positives and Negatives
3. Combine the sign with the difference for your answer

Rules for adding a Positive and Negative that a Mathematician could live with

2. When adding two numbers with different signs

1. Take the sign of the larger Absolute Value

2. Find the difference in the Absolute Values

3. Combine the sign of the larger Absolute Value with the difference in the two Absolute Values

finding the sign of the largest absolute Value

finding difference in absolute values & combining with the sign

Operation Subtraction

To successfully model subtracting integers it is important to remember the rules for addition. If students don’t have a solid grasp of the rules of adding integers your just wasting your time.

Positive - Positive = Positive

This first example of subtracting integers will be the easiest. This is what your teachers taught you in elementary school.

Let’s say we have a group of 5 Green soldiers (+5) and you take away 2 of these Green soldiers (+2). (Perhaps they were redeployed to a different area with more fighting.) The result of having 5 Green soldiers ((+5) and taking away 2 green soldiers (+2) is that 3 green soldiers remain (+3). So (+5) - (+2) = (+3).

The result is only 3 green soldiers (+3) remain

Positive - Positive = Negative

Sometimes when you subtract two positives you get a negative answer. A LOT of kids struggle with this. This is were understanding the rules for addition are critical.

To model this problem we can imagine a battlefield in which we have 6 Green soldiers (+6) and 4 Tan soldiers (-4) locked in combat. At this moment on the battlefield the Green soldiers have a 2 soldier advantage (+2). This battle scene that we are starting with equals a Positive 2 (+2).

For some reason three of the green soldiers leave (captured? Transferred to fight elsewhere?). So, we started this battle with a 2 soldier advantage (+2) for the Green soldiers. 3 of the Green solders (+3) are taken away. This now leaves 3 Green soldiers (+3) and 4 Tan soldiers to battle it out. The result of these 3 Green soldiers leaving it that Tan soldiers now have a 1 soldier advantage (-1). So (+2) - (+3) = (-1).

In this initial battle the green soldiers have a 2 soldier advantage (+2)

The result of taking away 3 green soldiers (+3) from a situation where the green had a 2 soldier (+2) advantage is that the tan now has a 1 soldier advantage (-1)

IMPORTANT THING TO NOTICE!

In the above battle, three Green soldiers (+3) are taken away to give the Tan soldiers a 1 soldier advantage (-1). But, what if the Green soldiers didn’t leave? What could we do to give the Tan soldiers the advantage by One? We could have given the Tan soldiers 3 more men (-3).

So a key thing to notice:

Taking away 3 Green soldiers (subtracting a positive 3) has the same result as adding 3 Tan soldiers (adding a negative 3). In both cases you get a one soldier advantage for the Tan army (-1).

Other examples:

(+5) - (+9) = (-4) is the same as (+5) + (-9) = (-4)

(+3) - (+5) = (-2) is the same as (+3) + (-5) = (-2)

Positive - Negative = Positive

In our next conflict, we have a total of 6 Green soldiers and 4 Tan soldiers doing battle. That would equal a positive 2 (+2) or a two soldier advantage for the Green at the start of this battle.

So we are starting with a 2 soldier advantage for the Green (+2). For some unexplained reason three of the Tan soldiers leave (probably retreating). As a result, the Green soldiers now have the advantage by 5 soldiers (6 Green vs. 1 Tan). So, (+2) - (-3) = (+5).

ANY TIME YOU SUBTRACT A NEGATIVE YOUR ANSWER WILL GET LARGER

(Any time you get rid of a negative in your life (expenses for example) your life gets better)

In this initial battle the green have a 2 soldier advantage (+2)

Next, three of the tan soldiers (-3) are taken away

The result of taking away 3 tan soldiers (-3) is that the green soldiers now have a 5 soldier (+5) advantage

IMPORTANT THING TO NOTICE!

In the above battle, three Tan soldiers (-3) are taken away to give the Green soldiers a 5 soldier advantage (+5). But, what if the Tan soldiers stayed? What could we do to give the Green soldiers the advantage by 5? We could have given the Green soldiers 3 more men (+3).

So a key thing to notice:

Taking away 3 Tan soldiers (subtracting a negative 3) has the same result as adding 3 Green soldiers (adding a positive 3). In both cases you get a five soldier advantage for the Green army (+5).

Other examples:

(+9) - (-5) = (+14) is the same as (+9) + (+5) = (+14)

(+13) - (-7) = (+20) is the same as (+13) + (+7) = (+20)

Negative - Negative = Negative

In our next clash of Green soldiers vs. Tan soldiers we have 2 Green and 5 Tan soldiers. So at the start of this fight, the Tan soldiers have the advantage by 3 soldiers (-3). As the battle rages, 2 of the tan soldiers (-2) leave to go fight somewhere else. Now the advantage the Tan soldiers have has been reduced to just a one soldier advantage (-1). So (-3) - (-2) = (-1).

We start with this battle where the tan soldiers have the advantage by 3 soldiers (-3)

The result of taking away two tan (-2) soldiers is an advantage for the tan soldiers of just 1 (-1)

IMPORTANT THING TO NOTICE!

In the above battle, two Tan soldiers (-2) are taken away resulting in just a 1 soldier advantage. But, what if the Tan soldiers never left? We could create the same outcome by reinforcing the Green soldiers with two more soldiers (+2).

So a key thing to notice:

Taking away 2 Tan soldiers (subtracting a negative 2) has the same result as adding 2 Green soldiers (adding a positive 2). In both cases you get a one soldier advantage for the Tan army (-1).

Other examples:

(-4) - (-2) = (-2) is the same as (-4) + (+2) = (-2)

(-20) - (-5) = (-15) is the same as (-20) + (+5) = (-15)

Negative - Negative = Positive

This is another situation that students really struggle to understand.

In this skirmish there are 4 Green soldiers (+4) and 5 Tan soldiers (-5) engaged in an epic conflict. At the start of this fight the Tan soldiers have a 1 soldier advantage (-1). In the middle of the fight 3 of the tan soldiers (-3) leave (why? I’m not really sure but I’m sure they had a good reason). When this happens the the Green soldiers now have an advantage by 2 soldiers (+2). So (-1) - (-3) = (+2). Just like in the previous examples, anytime you subtract a negative your answer will get larger.

The tan sarts off with a 1 soldier (-1) advantage

3 of the tan soldiers (-3) are taken away

the result of taking away 3 tan soldiers (-3) is a 2 soldier advantage for the green (+2)

IMPORTANT THING TO NOTICE!

In the above fight, three Tan soldiers (-3) are taken away resulting in just a 2 soldier advantage for the Green (+2). But, what if the Tan soldiers never left? We could create the same outcome by reinforcing the Green soldiers with three more soldiers (+3).

So a key thing to notice:

Taking away 3 Tan soldiers (subtracting a negative 3) has the same result as adding 3 Green soldiers (adding a positive 3). In both cases you get a two soldier advantage for the Green army (+2).

Other examples:

(-4) - (-7) = (+3) is the same as (-4) + (+7) = (+3)

(-15) - (-25) = (+10) is the same as (-15) + (+25) = (+10)

Negative - Positive = Negative

In our final conflict we have 5 tan soldiers (-5) and 2 green soldiers (+2) locked in an epic struggle. At this point the Tan soldiers have an advantage by 3 soldiers (-3). As the battle takes place, one of the Green soldiers (+1) leaves now creating a situation where there are now 4 more Tan soldiers (-4) than Green soldiers (5 Tan vs. 1 Green). So (-3) - (+1) = (-4)

This is another situation that kids really struggle with. Many will look at (-3) - (+1) and assume that it will equal (-2). Anytime you subtract a positive you will get a smaller answer, but students will often get confused and think that (-2) is smaller than (-4).

at the start of this battle the tan have the green outnumbered 5 to 2 for a 3 tan soldier advantage (-3).

the result of taking away 1 green soldier (+1) is a 4 soldier advantage for the tan (-4)

IMPORTANT THING TO NOTICE!

In the above fight, one Green soldier (+1) is taken away resulting in a 4 soldier advantage for the Tan (-4). But, what if the Green soldier never left? We could create the same outcome by reinforcing the Tan soldiers with one more soldier (-1).

So a key thing to notice:

Taking away 1 Green soldier (subtracting a positive 1) has the same result as adding 1 Tan soldier (adding a negative 1). In both cases you get a four soldier advantage for the Tan army (-4).

Other examples:

(-4) - (+3) = (-7) is the same as (-4) + (-3) = (-7)

(-11) - (+8) = (-19) is the same as (-11) + (-8) = (-19)

RULES FOR SUBTRACTION

In the subtraction problems above I have include a section called “IMPORTANT THING TO NOTICE!.” In each of these problems I showed how we could add the opposite of what we are subtracting and get the same answer. The is a key part of solving subtraction problems.

Convert Subtraction Problems to Addition problems then solve

Step 1: Change the subtraction sign into addition sign
Step 2: Change the sign of the second number
- DO NOT change the sign of the first number!!
Step 3: Follow the rules for Addition

This will work on all subtraction problems. In a few situations like a positive minus a smaller positive (example: 5 - 3) you will probably not convert to an addition problem, but you could.

Examples of changing Subtraction problems to Addition:

(+6) - (+9) can be changed to (+6) + (-9) both equal (-3)

(+13) - (-7) can be changed to (+13) + (+7) both equal (+20)

(-8) - (+3) can be changed to (-8) + (-3) both equal (-11)

(-70) - (-9) can be changed to (-70) + (+9) both equal (-61)